跨多种老化条件下的电池寿命预测:基于电池间深度学习的创新方法
- 论文翻译
- 2025-01-22
- 883热度
- 0评论
声明
本文档仅供学术交流与学习使用,若涉及版权问题,请联系我删除。
日期:2025 年 1 月 22 日
跨多种老化条件下的电池寿命预测:基于电池间深度学习的创新方法
接收日期:2023年12月6日
接受日期:2024年12月12日
在线发布:2025年1月15日
查看更新
Han Zhang \(^{1,2,4}\),Yuqi Li \(oplus^{1,3,4}\),Shun Zheng \(^{1}\)\(^{1 pi}\),Ziheng Lu \(^{1}\),Xiaofan Gui \(oplus^{1}\),Wei Xu \(^{2}\) & Jiang Bian © \(^{1}\)
摘要
在早期循环中准确预测电池寿命在实际应用中具有巨大价值。然而,由于影响电池容量复杂退化的多种因素(如循环协议、环境温度和电极材料),这一任务面临重大挑战。此外,在特定条件下进行循环测试既耗费资源又耗时。现有的预测模型主要在有限的老化条件下开发和验证,因此其广泛适用性存疑。本文提出了一种深度学习框架——BatLiNet,旨在可靠地预测多种老化条件下的电池寿命。其独特设计在于整合了电池间学习机制,用于预测两个电池单元之间的寿命差异。该机制与传统单电池学习相结合,增强了目标电池在不同老化条件下寿命预测的稳定性。基于广泛老化条件的实验结果表明,与现有模型相比,BatLiNet具有更高的准确性和鲁棒性。BatLiNet还展示了跨不同电池化学体系的迁移能力,为资源有限的场景提供了便利。我们期望这项研究能够促进跨电池洞察的探索,并推动电池研究在全面老化因素下的发展。
凭借高能量密度和低生产成本,锂离子电池已在现代工业中广泛应用,推动了可再生能源解决方案和电动汽车的发展 \(^{1-3}\)。然而,由于其固有的电化学机制,锂离子电池的容量在循环操作中不可避免地衰减 \(^{4}\)。意外的快速退化不仅会导致用户体验不佳(如电动汽车的续航焦虑),还可能影响关键设施(如电网稳定性)的运行。为了主动缓解这些副作用,准确预测电池在早期循环中的寿命已被确定为一项关键任务 \(^{5-8}\),其中寿命通常以循环寿命衡量,定义为电池容量降至其标称容量 \(80\%\) 时的充放电循环次数 \(^{9,10}\)。在早期循环中预测电池寿命极具挑战性,因为包括但不限于循环协议、环境温度和电极材料在内的众多因素共同影响着电池复杂的老化过程。此外,全面覆盖各种老化条件的成本和时间投入巨大,因为在特定条件下测试电池是一个漫长的过程。
[^0]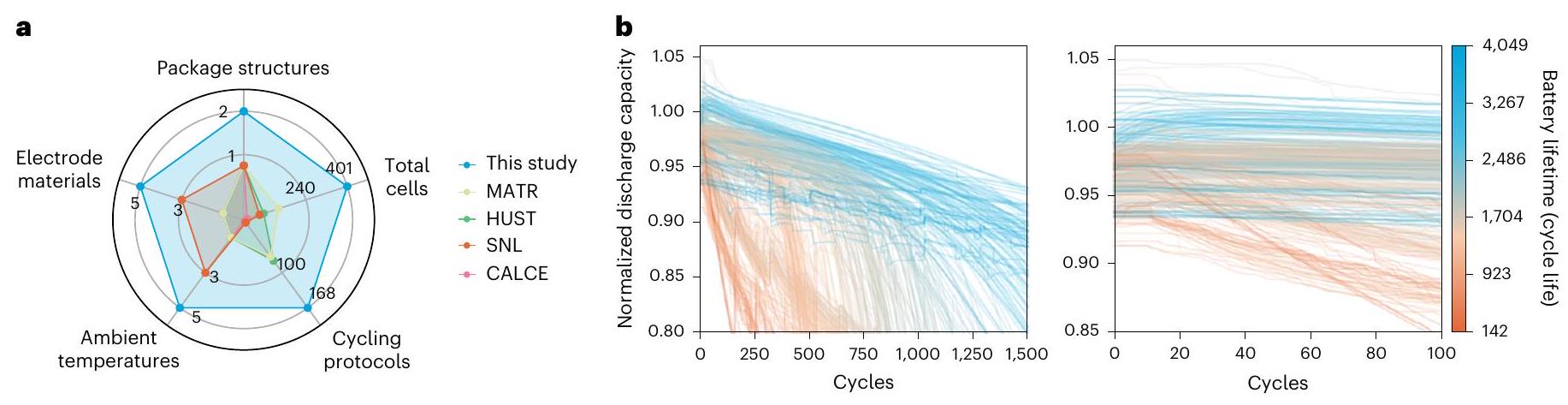
图1 | 本研究中涵盖的多种老化条件及其相关的复杂退化行为。a,我们将本研究中不同老化因素的广泛覆盖范围与典型数据集(包括MATR \(^{9}\)、HUST \(^{12}\)、SNL \(^{19}\) 和 CALCE \(^{13-15} \cdot \mathbf{b}\))进行了比较。b,长期和短期循环中容量退化的不同行为。
现有的电池寿命预测方法主要在有限的老化条件下开发和验证,例如仅测试磷酸铁锂(LFP)正极材料并使用某一组循环协议 \({ }^{9-12}\)。这些受限条件下的数据特征影响了特征设计和建模技术的全面检验,可能限制其结论的成功和泛化。这些方法在广泛老化条件下是否表现良好仍存疑问。此外,关注有限老化条件限制了利用在不同条件下收集的历史数据进行研究的发展。这一限制使得强调不同老化因素的电池数据集成为孤岛,阻碍了通用建模方法的发展。
在本研究中,我们提出了BatLiNet,这是一种深度学习框架,旨在可靠地预测多种老化条件下的电池寿命,例如循环协议、环境温度甚至电池化学体系的变化。该框架的核心是引入了电池间学习机制,通过对比成对电池单元来识别寿命差异,这是对传统仅关注单个电池模型的重大突破。通过将这种方法与传统的单电池学习相结合,BatLiNet不仅捕捉了单个电池的独特退化模式,还将这些模式置于更广泛的比较老化背景中。
在我们的实验中,涵盖了多种老化复杂性,BatLiNet始终优于传统模型,提供了精确且稳健的寿命预测。一个值得注意的观察是,BatLiNet能够将其单电池学习对应物的平均绝对百分比误差(MAPE)平均减少超过40%,这凸显了跨电池学习的重要性。此外,BatLiNet展示了在不同电池化学之间转移学习的有趣能力。这些发现强调了在电池数据建模中考虑广泛老化条件的重要性,并揭示了利用不同老化条件之间联系的未开发潜力。
结果
为了全面了解各种老化因素及其对电池寿命的影响,我们汇总了大多数公开可用的数据集,包括MATR \(^{9}\), \(\mathrm{HUST}^{12}\), \(\mathrm{CLO}^{11}\), \(\mathrm{CALCE}^{13-15}\), \(\mathrm{HNEI}^{16}\), UL-PUR \(^{17}\), RWTH \(^{18}\) 和 SNL \(^{19}\)。图1比较了本研究中检查的老化条件与典型数据集,突出了相关的复杂退化行为。补充说明1提供了所有数据集的额外详细比较。
在本研究中,我们导出了反映老化条件不同变化的五个数据集。首先,我们继承了MATR数据集的两个评估集,标记为MATR-1和MATR-2,以保持与现有模型的一致比较。此外,我们考虑了HUST数据集,使用与MATR相似的LFP电池,以研究当前模型对不同循环协议的适应性。此外,由于其他条件下的电池数量有限,我们通过将所有数据集合并为一个MIX集来包括其他数据集,这些条件包括不同的环境温度、包装结构和正极活性材料,如锂镍钴锰氧化物(NMC)、锂钴氧化物(LCO)和锂镍钴铝氧化物(NCA)。我们基于MIX数据集开发了两个预测设置:MIX-100和MIX-20。MIX-100检查了一个典型的早期预测场景,其中模型必须仅使用前100个循环的数据来预测80%的寿命终点。MIX-20提出了一个更具挑战性的任务,其中模型必须仅使用前20个循环来预测容量降至初始值90%之前的循环次数。值得注意的是,在早期循环中过早达到寿命终点的电池被排除在研究之外。
BatLiNet框架
众多老化条件与有限的电池循环覆盖之间的固有冲突对预测建模构成了重大挑战。现有模型主要关注电池内学习,捕捉单个电池的早期变化以预测其长期寿命 \(^{9,10}\)。然而,由于可用的电池样本有限,这种方法在数据稀缺方面存在困难。相比之下,我们的BatLiNet框架,如图2所示,集成了跨电池学习,这本质上是一个辅助任务,即给定一对电池预测寿命差异。我们将寿命未知的电池指定为“目标电池”,并使用现有数据库中的完全循环电池作为“参考电池”。
图2a描述了构建电池内和跨电池学习有效特征的过程,其中我们使用放电阶段的电压-容量曲线作为典型的循环级特征。传统的电池内学习方法在单个电池上操作,并通过计算一对早期循环之间的循环级特征差异来获得有效的电池内特征 \(^{9,10}\)。我们将这些操作称为计算电池内差异。相比之下,我们通过对比目标电池和参考电池在同一循环中的循环级特征来计算跨电池差异。跨电池差异旨在表示在不同条件下循环的电池之间的联系。
图2b展示了在不同老化条件下,电池单元内和电池单元间学习的潜力与挑战。上方的图表描绘了不同LFP电池组的标准偏差与相应寿命之间近乎线性的关系。虽然这种线性关系与之前的研究一致\({ }^{9}\),但该相关性也凸显了多样化老化条件带来的复杂性,如散点、异常值以及由于不同测试协议和温度导致的明显簇群所示。相反,下方的图表通过映射电池单元间差异与相关寿命差异之间的相关性,深入探讨了电池单元间学习。在此,相同的LFP电池作为目标电池,而一个共享的LCO电池作为参考。尽管面临多种老化因素的挑战,两者间的清晰联系依然可见。这表明,即使在参考电池来自不同化学体系的情况下,基于电池单元间差异曲线计算的简单特征也能区分寿命差异。补充说明2通过更多数据驱动的证据,进一步支持了在相同或不同电池化学体系内进行电池单元间学习的可行性。
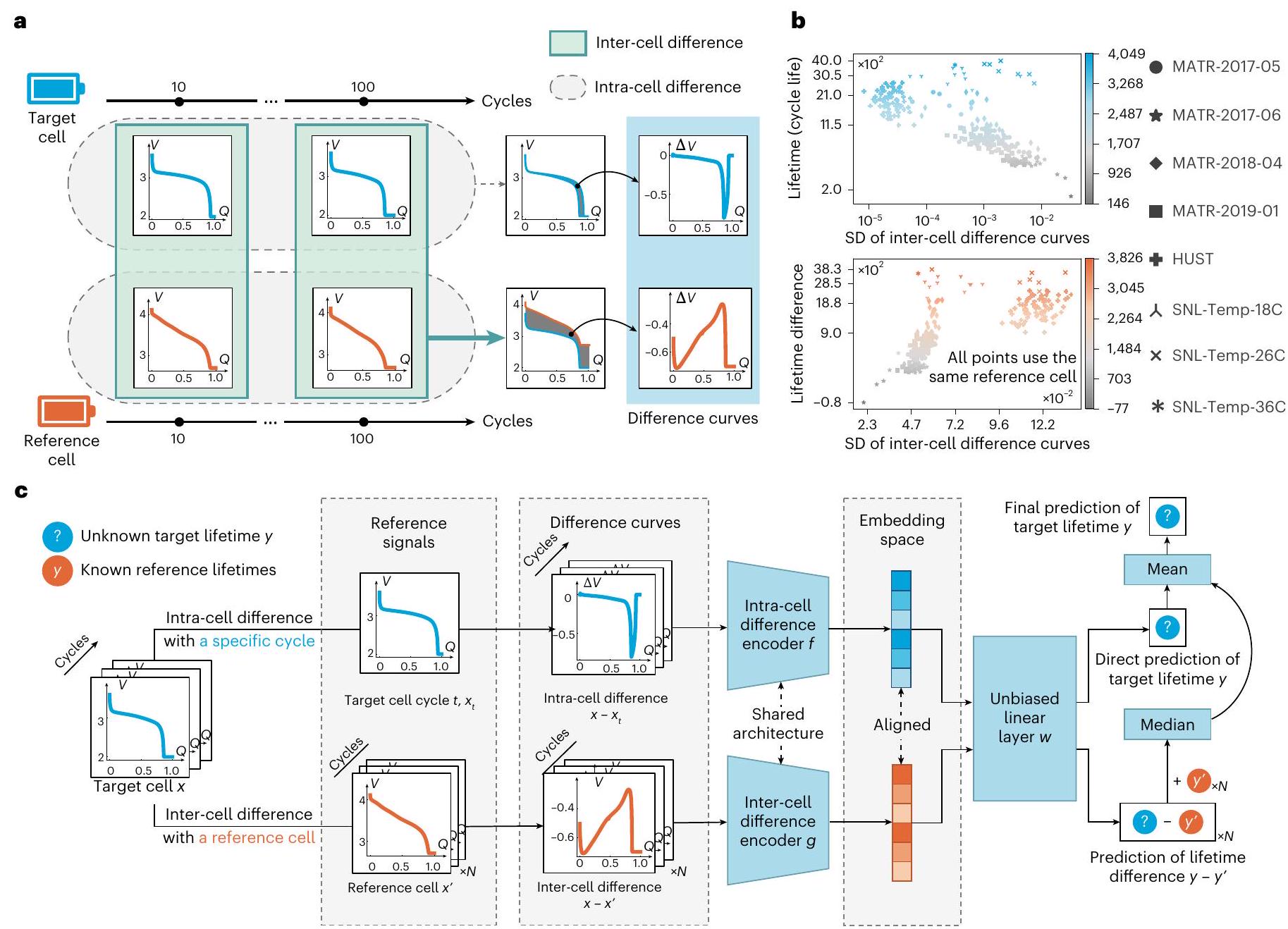
图2 | BatLiNet框架概览。a,基于展示 \(Q\)(当前容量与标称容量的比值)与 \(V\) 的关系(电压,单位伏特)关系的曲线,构建用于电池内和电池间学习的特征,作为每周期特征图。b,构建特征与预测目标之间的相关性,上半部分为电池内学习,下半部分为电池间学习。c,BatLiNet的数据流。
此外,这些非线性模式表明,利用深度学习进行有效表征学习的必要性。图2c总结了BatLiNet的数据流。给定目标电池,我们将其周期级特征输入两个独立分支。第一分支通过比较所有早期周期与参考周期的特征来计算电池内差异曲线,并使用特定神经网络\(f\)进行电池内学习。第二分支则包含一个参考电池以获取电池间差异曲线,并进一步将其输入另一个神经网络\(g\)进行电池间学习。经过 \(f\) 和 \(g\) 的编码过程后,所得表征被映射到一个对齐的线性空间,使我们能够利用共享的线性层为这两个分支生成输出。分离编码后接共享线性层的理由详见方法部分。训练过程中,我们可以简单地从训练集中选择任意一对电池,以激发跨多种老化条件组合的鲁棒电池间建模。为确保推理时的预测稳健性,我们从训练集中随机选取一批参考电池,并使用电池内和电池间分支输出的平均值作为最终预测。
图3展示了BatLiNet与不同数据集上最先进基线的比较,采用均方根误差(r.m.s.e.)和平均绝对百分比误差(MAPE)两个指标。可以看出,依赖手工特征的基本线性模型,如'Var.'、'Dis.'和'Full'模型,在各自初始数据集上表现优异。然而,面对包含复杂老化条件的数据集时,其性能显著下降。这一趋势也体现在一些应用于原始容量-电压曲线的高级统计学习技术上,如岭回归、偏最小二乘回归、主成分回归和支持向量机。随机森林是个例外,即使在MIX-100和MIX-20数据集上也能持续提供相对稳健的预测。尽管如此,随机森林在所有评估数据集上的表现普遍欠佳。
与统计方法相比,在参考文献10开发的特征空间中操作的深度学习模型,如多层感知器、长短时记忆网络和卷积神经网络(CNN),容易受到不同随机初始化导致的高变异性影响。这可能是由于可用于学习的电池数量有限,加之多样化的老化条件所致。
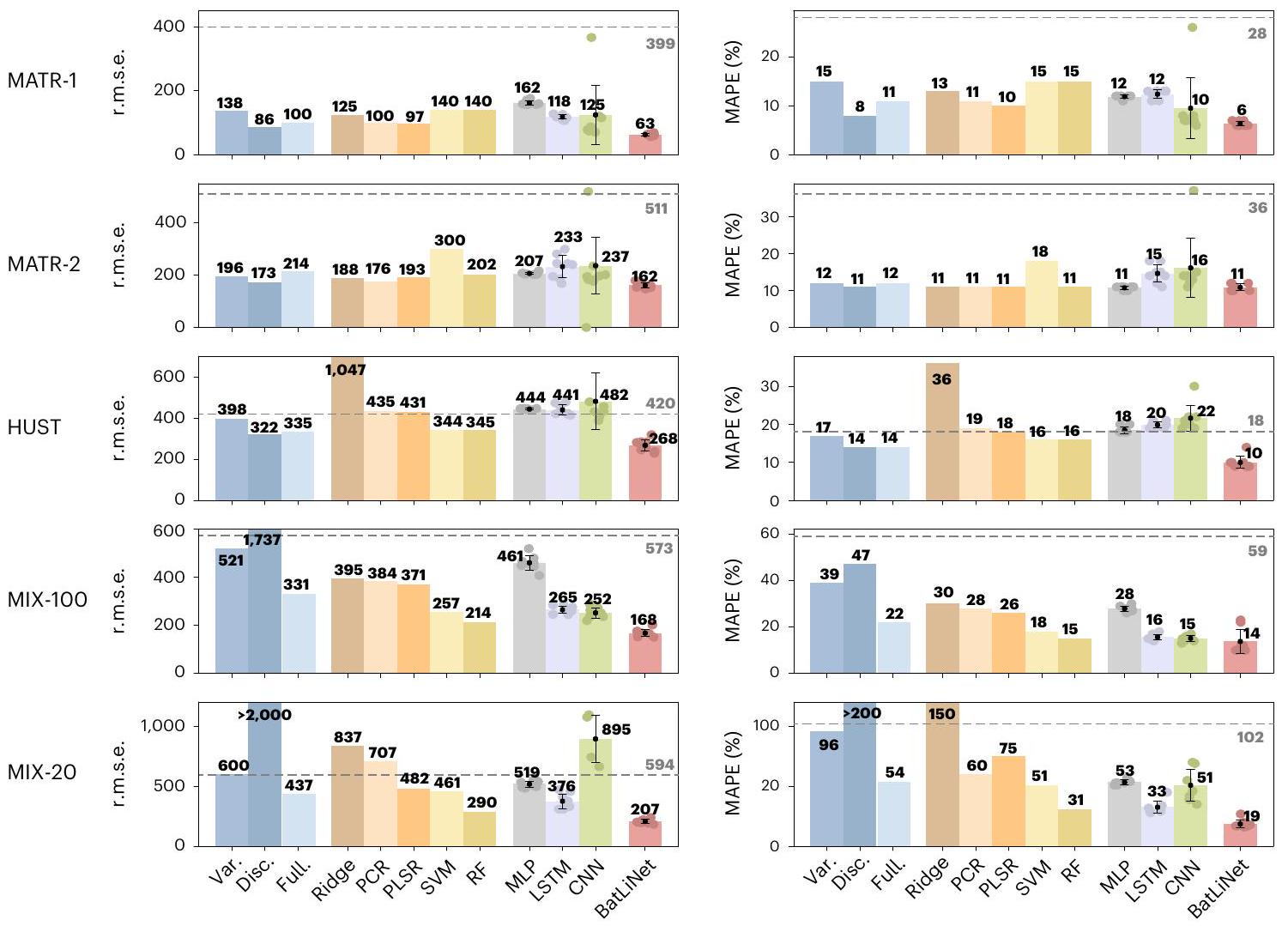
图3 | BatLiNet与线性模型、统计模型及深度学习模型的性能对比。线性模型(Var.、Dis.和Full)源自参考文献9,统计模型(岭回归、偏最小二乘回归、主成分回归、支持向量机、随机森林)和深度学习模型(多层感知机(MLP)、长短期记忆网络(LSTM)、卷积神经网络(CNN))则来自参考文献10。这些比较涵盖了五个数据集:MATR-1、MATR-2、HUST、MIX-100和MIX-20,并采用了两项评估指标:均方根误差(r.m.s.e.)和平均绝对百分比误差(MAPE)。对于深度学习模型,我们进行了八次独立初始化的实验(n=8次试验)。柱状图展示了平均值和标准差。虚线代表一个简单基线,即使用训练电池的平均寿命作为固定预测值,以体现学习的难度。PCR,主成分回归;PLSR,偏最小二乘回归;RF,随机森林;Ridge,岭回归;SVM,支持向量机。
在存在复杂老化模式和显著噪声的情况下,BatLiNet同样属于深度学习家族,并采用相同的CNN架构进行特征编码。我们观察到,它显著缓解了与深度学习基线相关的高变异性,在不同老化条件下始终提供极具竞争力的结果。具体而言,BatLiNet将表现最佳的基线(因数据集而异)的r.m.s.e.分别降低了\(36.5\), \(6.8\), \(20.1\), \(27.4\) 和 \(40.1\%\)。与单电池学习的对应模型CNN相比,BatLiNet能将平均MAPE降低多达$40%$。值得注意的是,即便对于BatLiNet,MIX-100和MIX-20数据集上的MAPE得分也明显高于MATR-1和MATR-2等先前数据集。我们认为,这凸显了在电池数据建模中考虑全面老化因素的重要性。
此外,我们深入探讨了BatLiNet的跨化学体系迁移能力。具体来说,我们旨在确认BatLiNet是否能增强从资源丰富的化学体系向其他电池化学体系(拥有有限电池样本)的迁移。这一安排可以突显其在加速未来化学体系精确寿命预测方面的潜力。实验中,我们使用275个LFP电池作为资源丰富的化学体系,目标是探究如何有效利用这些LFP电池为剩余的37个LCO电池、22个NCA电池和69个NMC电池开发模型。为了评估的一致性,我们随机抽取了21个LCO电池、14个NCA电池和53个NMC电池组成各自的测试集。然后,从剩余电池中分别抽取$1,2,4,8$和16个电池作为模型训练的数据,对应每种目标电池化学体系的不同低资源条件。图4展示了这些模型的总体比较结果。可以看出,在大多数情况下,BatLiNet相较于其他学习模型展现了明显的误差降低。例如,直接学习无法利用LFP电池的信息,因此在目标电池数量极少时表现不佳。基于参数的迁移学习依赖于预训练参数实现隐式迁移,但我们发现其在某些情况下也可能面临泛化挑战,比如从LFP电池迁移到仅有一个NCA或LCO电池的情况。相比之下,BatLiNet通过电池间学习实现了显式迁移,在大多数情况下提供了更稳健和准确的预测。
最后,我们解释了BatLiNet中的参考选择策略。图5展示了MIX-100数据集的扩展结果。图5a显示,为目标电池选择参考电池会显著影响预测误差,这一点从不同测试集电池的最佳与最差选择之间的差距可见一斑。虽然选择最优参考电池具有挑战性,但我们通过采样一批参考电池并使用它们的中位数预测来缓解性能波动,如图5b所示。图5c揭示,随着批量大小呈指数增长,这种批量采样机制确实会导致推理速度显著下降。然而,考虑到电池循环时间较长,这些推理速度上的差异可以忽略不计。我们发现,使用64个参考电池的批量能在保持合理推理速度的同时,提供稳健的预测。
讨论
我们介绍了BatLiNet,一个整合了电池间与电池内学习的深度学习框架,旨在提升跨不同老化条件下的电池寿命预测。电池间学习作为补充,
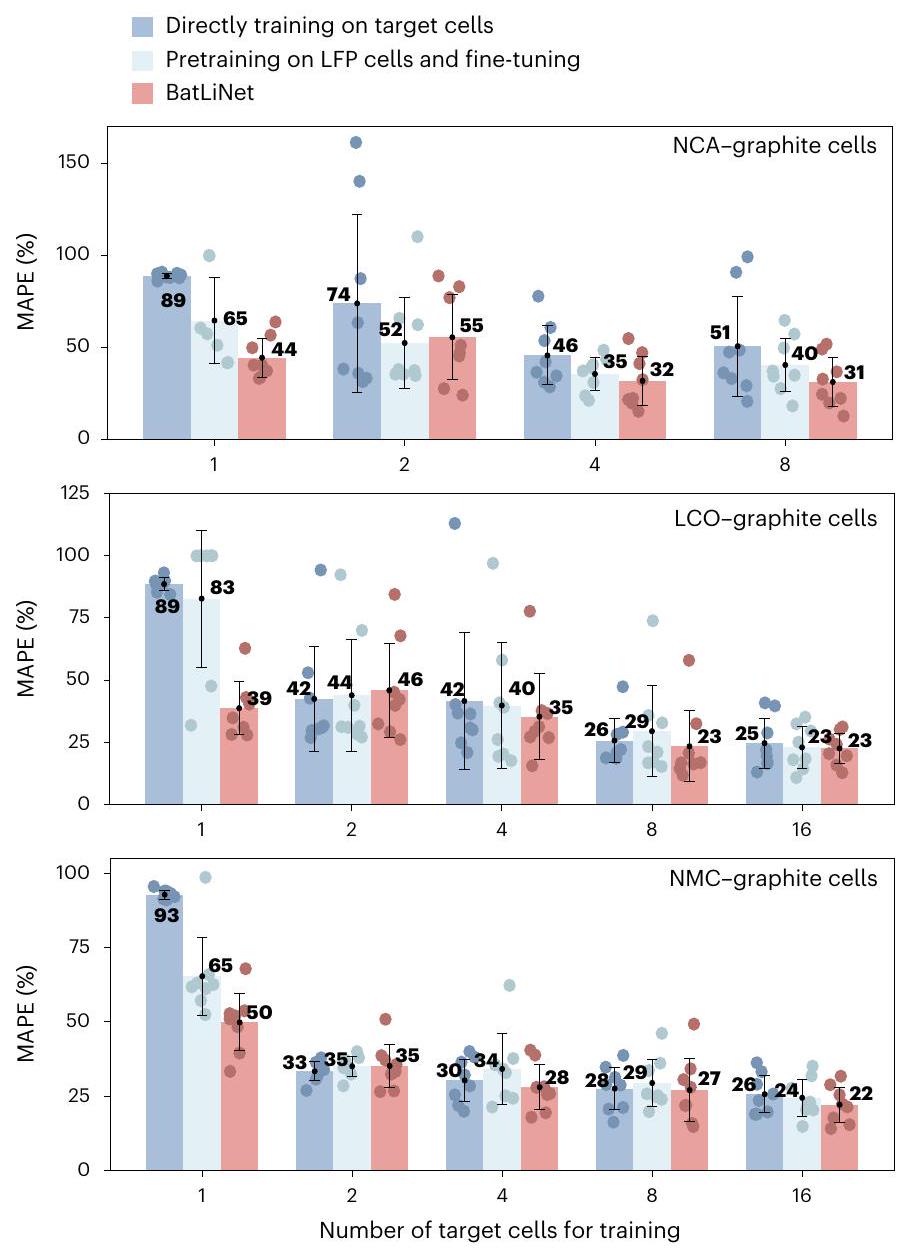
图4 | BatLiNet在从275个LFP电池转移到有限的NCA、LCO和NMC目标电池时的性能比较。我们通过改变可用于训练的目标电池数量(\(1,2,4,8,16\))来模拟各种低资源场景。BatLiNet的跨电池学习与两个基线进行了比较:直接在目标电池上训练的CNN模型和在LFP电池上预训练然后微调的CNN模型。每种情况和模型都经过八次独特的初始化和数据分割测试(\(n=8\)次试验),柱状图显示平均误差,误差条表示运行间的标准偏差。
通过实现不同老化条件下的知识转移,该方法具有潜在的应用价值,例如估计电池的充电状态和健康状态 \(^{5,28}\),适应快速充电协议 \(^{29}\) 等多样化老化条件,以及适应固态和钠离子电池 \(^{30-32}\) 等新兴化学体系,预测实际条件下的日历寿命以实现更准确的寿命估计 \(^{33}\)。
尽管本研究展示了跨多种条件下跨电池学习的数据驱动可行性,但更深入的物理理解和建模仍然是必要的 \(^{34}\)。未来的研究应优先考虑全面理解和建模多样化老化因素的方法,以推动电池的研究、开发和应用。
方法
构建每周期特征图
我们使用归一化容量(\(Q \in [0,1]\))作为统一指标,以对齐不同周期中的不同电信号,并计算它们在相同阶段或充放电阶段之间的差异。这样,我们无需担心不同周期和充放电阶段中不同信号的可变长度。此外,由于电信号的冗余记录,我们可以通过对原始时间索引信号进行插值来获得这些 \(Q\) 索引的序列,并通过调整插值粒度轻松控制特征维度。在此步骤之后,我们可以获得四种类型的处理序列,分别由 \(Q\), \(V_{\mathrm{c}}(Q)\), \(V_{\mathrm{d}}(Q)\), \(I_{\mathrm{c}}(Q)\) 和 \(I_{\mathrm{d}}(Q)\) 索引,其中 \(Q\) 从 0 到 1 变化,步长预先指定,\(V\) 表示电压,\(I\) 表示电流,\(\mathrm{d}\) 和 \(\mathrm{c}\) 是上标,分别表示放电和充电阶段。我们进一步推导出两个额外的信号来表征充放电阶段之间的联系:(1)\(\Delta V(Q) = V_{\mathrm{c}}(Q) - V_{\mathrm{d}}(Q)\),表示充电电压和放电电压之间的差距,以及(2)\(R(Q) = \left(V_{\mathrm{c}}(Q) - V_{\mathrm{d}}(Q)\right) / \left(I_{\mathrm{c}}(Q) - I_{\mathrm{d}}(Q)\right)\),对应于 \(Q\) 变化时内阻的状态。这些周期级特征作为计算电池内和电池间差异的基本元素。
确保从周期级特征图计算这些差异的有效性有两个关键处理步骤。首先是通过各自的标称容量对所有电池的容量进行归一化,确保 \(Q\) 的范围落在 \([0,1]\) 内,以适应具有非常不同标称容量的各种电池类型。其次是消除由于循环协议的变化而引入的电流和电压信号突变的噪声。我们使用基于滚动中值的滤波器来缓解这个问题:
\(\begin{aligned}
\mathbf{M} &= \text{rolling_median}(\mathbf{r}, w) \\
\Delta \mathbf{M} &= \text{abs}(\text{rolling_median}(\mathbf{M}, w)) \\
r_t^{\text{new}} &=
\begin{cases}
M_t & \text{if } \Delta M_t > 3 \times \operatorname{median}(\Delta \mathbf{M}) \\
r_t & \text{otherwise}
\end{cases}
\end{aligned}
\)
这里\(mathbf{r}\)是原始信号,\(w\)表示滚动操作的窗口大小。这些多方面的特征图将作为单独的通道用于电池内和电池间学习。
统一电池内和电池间学习
给定电池单元的电池内特征,记为 \(\mathbf{x}\),及其循环寿命 \(y\),我们希望优化以下目标以获得完美的循环寿命预测器。
\(\begin{equation}
\min_{\theta} \mathbb{E}_{(\mathbf{x}, y) \in D}\left|f_{\theta}(\mathbf{x})-y\right|_{2}^{2}, \tag{4}
\end{equation}
\)
其中,\(D\) 表示数据分布,\(f_{\theta}\) 是由参数 \(\theta\) 参数化的编码函数,\(\mathbf{w}_{f}\) 是最后一层预测层的权重。实际上,我们需要在有限的训练实例上进行经验风险最小化,即
\(\begin{equation}
\min_{\theta} \sum_{i=1}^{N}\left|f_{\theta}\left(\mathbf{x}_{i}\right)-y_{i}\right|_{2}^{2} . \tag{5}
\end{equation}
\)
然而,电池寿命预测是一个特殊的任务,由于非线性建模的必要性和获取数据标签的巨大成本,它面临着数据稀缺的挑战。在这种情况下,将 \(f_{\theta}\) 实例化为神经网络存在较高的过拟合风险。为了缓解数据稀缺问题,我们考虑对两个不同电池之间的差异进行建模:
\(\begin{equation}
\min_{\theta} \mathbb{E}_{(\Delta x, \Delta y)}\left|g_{\phi}(\Delta \mathbf{x})-\Delta y\right|_{2}^{2}, \tag{6}
\end{equation}
\)
其中 \(\Delta \mathbf{x}=\mathbf{x}-\mathbf{x}^{\prime}, \Delta y=y-y^{\prime},(\mathbf{x}, y)\) 和 \(\left(\mathbf{x}^{\prime}, y^{\prime}\right)\) 是从 \(D\) 中独立采样的,\(g_{\phi}\) 是由 \(\phi\) 参数化的函数,作用于 \(\Delta \mathbf{x}\) 的空间。
图 \(5 \text{ mid}\) BatLiNet 中参考电池选择的分析。a, 使用遍历所有训练电池的单个参考电池,MIX-100 数据集中所有测试电池的最佳、最差和中位数预测误差。阴影区域表示随机选择参考电池时预测误差的标准差。\(\mathbf{b}\), 在 MIX-100 数据集中,增加参考电池数量对预测的影响,每种情况随机选择八次(\(n=8\) 次试验)。每个箱线图显示中位数为中心线,25% 和 75% 百分位数分别为下四分位数和上四分位数,须线延伸至四分位距的 1.5 倍,包括异常点。c, 在 NVIDIA GTX 4090 图形处理单元上测试,随着参考电池数量的增加,推理吞吐量的变化。
电池间学习公式 (6) 假设任何一对电池的特征表示差异与其寿命差异之间存在统一的关系。具体来说,我们可以在线性设置中建立 \(f_{\theta}\) 和 \(g_{\phi}\) 之间的明确联系。例如,如果 \(y\) 是零中心的(可以通过预处理实现),并且原始目标 (4) 的最优解是 \(f_{\theta^{}}(x) = \mathbf{w}^{T} \mathbf{x}\),那么很容易验证 \(g_{\phi^{}} = f_{\theta^{}}\) 也是对比目标 (6) 的最优解,因为 \(\mathbb{E}_{(\Delta x, \Delta y)}\left|\mathbf{w}^{* T} \Delta \mathbf{x} - \Delta y\right|_{2}^{2}\) 可以分解为
\(\begin{equation*}
\mathbb{E}_{(\mathbf{x}, y) \in D}\left\|\mathbf{w}^{* T} \mathbf{x}-y\right\|_{2}^{2}+\mathbb{E}_{\left(\mathbf{x}^{\prime}, y^{\prime}\right) \in D}\left\|\mathbf{w}^{* T} \mathbf{x}^{\prime}-y^{\prime}\right\|_{2}^{2} \tag{7}
\end{equation*}
\)
在非线性设定下,例如使用神经网络作为函数逼近器时,建立\(f{\theta}\)与\(g{\phi}\)之间的精确联系变得棘手,这导致了两个独立的优化过程。受线性设定下目标(4)和(6)相同最优性的启发,我们提出在使用神经网络时共享\(f{\theta}\)和\(g{\theta}\)的最后一层线性层,即
\(\begin{equation*}
f_{\theta}(\mathbf{x})=\mathbf{w}^{T} h_{\theta}(\mathbf{x}), \quad g_{\phi}(\Delta \mathbf{x})=\mathbf{w}^{T} h_{\phi}(\Delta \mathbf{x}), \tag{8}
\end{equation*}
\)
其中\(\mathbf{w}\)是共享参数,\(h{\theta}(\cdot)\)和\(h{\phi}(\cdot)\)分别是由\(\theta\)和\(\phi\)参数化的两个独立神经网络。通过这种方式,我们可以通过共享参数\(w\)连接目标(4)和(6)的优化,并享受细胞内和细胞间建模之间的互补性。
此外,我们还需要执行经验风险最小化以模拟期望的目标(6)。具体来说,鉴于我们仅有\(N\)个训练实例,我们使用\(N(N-1)\)对实例来替代独立采样实例对的期望。结合原始回归,我们得到以下联合经验风险最小化问题:
\(\begin{equation*}
\min _{\mathbf{w}, \theta, \phi} \sum_{i=1}^{N}\left\|\mathbf{w}^{T} h_{\theta}\left(\mathbf{x}_{i}\right)-y_{i}\right\|_{2}^{2}+\lambda \sum_{i=1}^{N} \sum_{\substack{j=1 \\ j \neq i}}^{N}\left\|\mathbf{w}^{T} h_{\phi}\left(\Delta \mathbf{x}_{i, j}\right)-\Delta y_{i, j}\right\|_{2}^{2}, \tag{9}
\end{equation*}
\)
其中\(\Delta \mathbf{x}_{i j}=\mathbf{x}_{i}-\mathbf{x}_{j}\), \(\Delta y_{i j}=y_{i}-y_{j}\),\(\lambda\)是用于平衡两个回归目标的超参数。
优化阶段结束后,我们可以利用神经网络对细胞内和细胞间差异进行编码以做出预测。给定一个未见过的实例\(\mathbf{x}\),我们有
\(\begin{equation*}
\hat{y}^{o}=\mathbf{w}^{T} h_{\theta}(\mathbf{x}), \quad \hat{y}^{c}=\mathbf{w}^{T} h_{\phi}\left(\mathbf{x}-\mathbf{x}^{\prime}\right)+y^{\prime}, \tag{10}
\end{equation*}
\)
其中 \(\hat{y}^{\rho}\) 和 \(\hat{y}^{c}\) 分别是在原始空间和对比空间中的预测,\(\left(\mathbf{x}^{\prime}, y^{\prime}\right)\) 可以从训练实例中采样得到。最后,我们将寿命预测为 \(\hat{y}=\alpha \hat{y}^{\circ}+(1-\alpha) \hat{y}^{c}\),其中 \(\alpha\) 是用于平衡两种预测类型的超参数。
Data availability
All datasets used in this study are publicly accessible and include MATR and CLO ( https://data.matr.io/1/ ), HUST ( https://data.mendeley.com/ datasets/nsc7hnsg4s/2), CALCE ( https://web.calce.umd.edu/batteries/ data) and RWTH ( https://publications.rwth-aachen.de/record/818642/ files). HNEI, SNL and UL-PUR datasets are hosted by BatteryArchive ( https://www.batteryarchive.org/study_summaries.html ). Moreover, we leverage an open-source tool, BatteryML ${ }^{35}$, to preprocess these datasets into a unified format to support experiments reported in this article.
Code availability
Our code is available on CodeOcean ${ }^{36}$, including instructions to train all models from scratch and to perform direct inference with our provided checkpoints.
References
- Tarascon, J. M. & Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 414, 359-367 (2001).
- Armand, M. & Tarascon, J. M. Building better batteries. Nature 451, 652-657 (2008).
- Dunn, B. S., Kamath, H. & Tarascon, J. M. Electrical energy storage for the grid: a battery of choices. Science 334, 928-935 (2011).
- Arora, P., White, R. E. & Doyle, M. Capacity fade mechanisms and side reactions in lithium-ion batteries. J. Electrochem. Soc. 145, 3647 (1998).
- Ng, M.-F., Zhao, J., Yan, Q., Conduit, G. J. & Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2, 161-170 (2020).
- Yao, Z. et al. Machine learning for a sustainable energy future. Nat. Rev. Mater. 8, 202-215 (2023).
- Biggio, L., Bendinelli, T., Kulkarni, C. & Fink, O. Ageing-aware battery discharge prediction with deep learning. Appl. Energy 346, 121229 (2023).
- Li, T., Zhou, Z., Thelen, A., Howey, D. A. & Hu, C. Predicting battery lifetime under varying usage conditions from early aging data. Cell Rep. Phys. Sci. 5, 101891 (2024).
- Severson, K. A. et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 4, 383-391 (2019).
- Attia, P. M., Severson, K. A. & Witmer, J. D. Statistical learning for accurate and interpretable battery lifetime prediction. J. Electrochem. Soc. 168, 090547 (2021).
- Attia, P. M. et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 578, 397-402 (2020).
- Ma, G. et al. Real-time personalized health status prediction of lithium-ion batteries using deep transfer learning. Ener. Environ. Sci. 15, 4083-4094 (2022).
- He, W., Williard, N., Osterman, M. & Pecht, M. Prognostics of lithium-ion batteries based on dempster-shafer theory and the bayesian monte carlo method. J. Power Sources 196, 10314-10321 (2011).
- Xing, Y., Ma, E., Tsui, K.L. & Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 53, 811-820 (2013).
- Williard, N., He, W., Osterman, M. & Pecht, M. Comparative analysis of features for determining state of health in lithium-ion batteries. Int. J. Progn. Health Manag. 4, 1-7 (2013).
- Devie, A., Baure, G. & Dubarry, M. Intrinsic variability in the degradation of a batch of commercial 18650 lithium-ion cells. Energies 11, 1031 (2018).
- Juarez-Robles, D., Jeevarajan, J. A. & Mukherjee, P. P. Degradation-safety analytics in lithium-ion cells: part I. Aging under charge/discharge cycling. J. Electrochem. Soc. 167, 160510 (2020).
- Li, W. et al. One-shot battery degradation trajectory prediction with deep learning. J. Power Sources 506, 230024 (2021).
- Preger, Y. et al. Degradation of commercial lithium-ion cells as a function of chemistry and cycling conditions. J. Electrochem. Soc. 167, 120532 (2020).
- Hoerl, A. E. & Kennard, R. W. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12, 55-67 (1970).
- Geladi, P. & Kowalski, B. R. Partial least-squares regression: a tutorial. Anal. Chim. Acta 185, 1-17 (1986).
- Jolliffe, I. T. Principal components in regression analysis. In Principal Component Analysis. Springer Series in Statistics 167-198 (Springer, 2002).
- Drucker, H. et al. Support vector regression machines. Adv. Neural Inform. Proc. Syst. 9, 155-161 (1996).
- Breiman, L. Random forests. Mach. Learn. 45, 5-32 (2001).
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signal. Syst. 2, 303-314 (1989).
- Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735-1780 (1997).
- Krizhevsky, A., Sutskever, I. & Hinton, G. E. Imagenet classification with deep convolutional neural networks. Commun. ACM 60, 84-90 (2012).
- Roman, D., Saxena, S., Robu, V., Pecht, M. & Flynn, D. Machine learning pipeline for battery state-of-health estimation. Nat. Mach. Intell. 3, 447-456 (2021).
- Zeng, Y. et al. Extreme fast charging of commercial li-ion batteries via combined thermal switching and self-heating approaches. Nat. Commun. 14, 3229 (2023).
- Randau, S. et al. Benchmarking the performance of all-solid-state lithium batteries. Nat. Energy 5, 259-270 (2020).
- Shraer, S. D. et al. Development of vanadium-based polyanion positive electrode active materials for high-voltage sodium-based batteries. Nat. Commun. 13, 4097 (2022).
- Li, Y. et al. Origin of fast charging in hard carbon anodes. Nat. Energy 9, 134-142 (2024).
- McBrayer, J. D. et al. Calendar aging of silicon-containing batteries. Nat. Energy 6, 866-872 (2021).
- Brosa Planella, F. et al. A continuum of physics-based lithium-ion battery models reviewed. Prog. Energy 4, 042003 (2022).
- Zhang, H. et al. BatteryML: an open-source platform for machine learning on battery degradation. Zenodo 10.5281/ zenodo. 14040125 (2024).
- Zhang, H. et al. Code for 'battery lifetime prediction across diverse aging conditions with inter-cell deep learning'. Code Ocean https://doi.org/10.24433/CO.8904065.v2 (2024).
Acknowledgements
The authors received no specific funding for this work.
Author contributions
H.Z. led the development of BatLiNet and conducted most experiments. Y.L. provided valuable insights into cross-chemistry and facilitated the experiment analysis. S.Z. led the overall research, built the initial code base and introduced the concept of inter-cell learning. S.Z., H.Z. and Y.L. wrote the paper. Z.L. contributed to refining the manuscript and inspiring cross-chemistry explorations. X.G. ensured the reproduction of all experiments and refined paper presentation. Both W.X. and J.B. participated in the discussion of ideas and analysis of results. J.B. provided overarching supervision for the research and strong support for the entire team.
Competing interests
The authors declare no competing interests.
Additional information
Supplementary information The online version contains
supplementary material available at
https://doi.org/10.1038/s42256-024-00972-x.
Correspondence and requests for materials should be addressed to Shun Zheng or Jiang Bian.
Peer review information Nature Machine Intelligence thanks Kandler Smith, Qingyu Yan and the other, anonymous, reviewer (s) for their contribution to the peer review of this work.
Reprints and permissions information is available at
www.nature.com/reprints.
Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons
Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author (s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in a credit line
to the material. If material is not included in the article's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/ licenses/by/4.0/.
(c) The Author (s) 2025
[^0]: ${ }^{1}$ Microsoft Research, Beijing, China. ${ }^{2}$ Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing, China. ${ }^{3}$ Present address: Department of Materials Science and Engineering, Stanford University, Stanford, CA, USA. ${ }^{4}$ These authors contributed equally: Han Zhang, Yuqi Li. ®e-mail: [email protected] ; [email protected]
